Solving Linear Algebra (LA) problems is a core task in four out of five EoCoE II Scientific Challenges (SC) and thus the availability of exascale-enabled LA solvers is fundamental in preparing the SC applications for the new exascale ecosystem. The goal of WP3 is to design and implement exascale-enabled LA solvers for the selected applications and to integrate them into the application codes. A co-design approach between LA and SC experts will be used; nevertheless, the solvers will be also developed in a more general perspective, to obtain LA tools useful for a wider range of applications. The LA experts involved in WP3 have a long-standing experience in developing solvers for HPC platforms, and the planned activities will build upon software and methodologies developed by them and tested during EoCoE I. New algorithms and disruptive technologies will be also considered, to tackle the new challenges posed by the envisioned exascale systems.
In order to achieve the previous goal, the following steps will be performed:
- analysis of the LA kernels of the applications, to clearly identify the needs of the applications in terms of LA solvers, and to select the best LA methodologies and software to work with. Actually, this work has been triggered during EoCoE I, providing a sound basis for EoCoE II
- extension, modification, and re-factoring of the selected LA solvers, based on a co-design approach between LA experts and application experts, to ensure that solvers and applications evolve accordingly in their route toward exascale
- design and implementation of novel solvers, for applications where modifying and re-factoring the available LA solvers does not appear satisfactory
- Integration of the LA solvers into the applications, in strict collaboration between LA and application experts, and testing and tuning on problems of interest
The work will address the Material, Water, Fusion and Wind Scientific Challenges, where strong needs for exascale-enabled LA solvers have emerged during EoCoE I. A different task for each SC has been planned, plus a task concerning transversal activities. The HPC packages developed by the LA experts participating in EoCoE II will provide a sound basis.
- Task 3.1 Scalable Solvers for Materials: Luc Giraud (INRIA)
- Task 3.2 Scalable Solvers for Water: Pasqua D’Ambra (CNR)
- Task 3.3 Scalable Solvers for Fusion: Ulrich Rüde (Cerfacs)
- Task 3.4 Scalable Solvers for Wind: Luc Giraud (INRIA)
- Task 3.5 Transversal activities: Alfredo Buttari (CNRS)
PSBLAS
The PSBLAS library, developed with the aim to facilitate the parallelization of computationally intensive scientific applications, is designed to address parallel implementation of iterative solvers for sparse linear systems through the distributed memory paradigm. It includes routines for multiplying sparse matrices by dense vectors, solving block diagonal systems with triangular diagonal entries, preprocessing of sparse matrices, parallel data exchange, mesh index handling and auxiliary operations on dense vectors.
It is available at https://psctoolkit.github.io/
AMG4PSBLAS
AMG4PSBLAS has been designed to provide scalable and easy-to-use preconditioners in the context of the PSBLAS (Parallel Sparse Basic Linear Algebra Subprograms) computational framework and is used in conjuction with the Krylov solvers available from PSBLAS. The package employs object-oriented design techniques in Fortran 2003, with interfaces to additional third party libraries such as MUMPS, UMFPACK, SuperLU, and SuperLU_Dist, which can be exploited in building multilevel preconditioners.
It is available at https://psctoolkit.github.io/
MUMPS
MUltifrontal Massively Parallel sparse direct Solver (MUMPS) is a parallel solver for sparse systems of linear equations. Based on the multifrontal method, MUMPS can solve square symmetric positive definite, symmetric indefinite and un-symmetric problems using the LDL T or the LU factorization of the system matrix. MUMPS provides a very wide range of features. Among these, the most significant is certainly the ability to use numerical pivoting in a parallel distributed memory setting which renders the solution method practically stable and thus reliable on a very wide set of problems. Other widely used features include computation of the Schur complement of a matrix, Out-Of-Core execution, computation of selected entries of the inverse of a matrix, system pre and post-processing facilities and, more recently, low-rank approximations. MUMPS uses MPI and OpenMP for achieving parallelism on distributed and shared memory parallel systems.
It is available at http://mumps-solver.org/
AGMG
AGMG (AGgregation-based algebraic MultiGrid) solves systems of linear equations with an aggregation-based algebraic multigrid method. It is expected to be efficient for large systems arising from the discretization of scalar second order elliptic PDEs. The method is however purely algebraic and may be tested on any problem.
AGMG has been designed to be easy to use by non experts (in a black box fashion). It is available both as a software library for FORTRAN or C/C++ programs, and as a Octave/Matlab function.
For more information and download, see http://www.agmg.eu/
Chameleon
Keywords: Runtime system – Task-based algorithm – Dense linear algebra – HPC – Task scheduling
Scientific Description: Chameleon is part of the MORSE (Matrices Over Runtime Systems @ Exascale) project. The overall objective is to develop robust linear algebra libraries relying on innovative runtime systems that can fully benefit from the potential of those future large-scale complex machines.
We advance in three directions based first on strong and closed interactions between the runtime and numerical linear algebra communities. This initial activity will then naturally expand to more focused but still joint research in both fields.
Functional Description: Chameleon is a dense linear algebra software relying on sequential task-based algorithms where sub-tasks of the overall algorithms are submitted to a Runtime system. A Runtime system such as StarPU is able to manage automatically data transfers between not shared memory area (CPUs-GPUs, distributed nodes). This kind of implementation paradigm allows to design high performing linear algebra algorithms on very different type of architecture: laptop, many-core nodes, CPUs-GPUs, multiple nodes. For example, Chameleon is able to perform a Cholesky factorization (double-precision) at 80 TFlop/s on a dense matrix of order 400 000 (e.i. 4 min).
Release Functional Description: Chameleon includes the following features:
– BLAS 3, LAPACK one-sided and LAPACK norms tile algorithms – Support QUARK and StarPU runtime systems and PaRSEC since 2018 – Exploitation of homogeneous and heterogeneous platforms through the use of BLAS/LAPACK CPU kernels and cuBLAS/MAGMA CUDA kernels – Exploitation of clusters of interconnected nodes with distributed memory (using OpenMPI)
- Partners: Innovative Computing Laboratory (ICL) – King Abdullha University of Science and Technology – University of Colorado Denver
- URL: https://gitlab.inria.fr/solverstack/chameleon
MAPHYS
Massively Parallel Hybrid Solver
Keyword: Parallel hybrid direct/iterative solution of large linear systems
Functional Description: MaPHyS is a software package that implements a parallel linear solver coupling direct and iterative approaches. The underlying idea is to apply to general unstructured linear systems domain decomposition ideas developed for the solution of linear systems arising from PDEs. The interface problem, associated with the so called Schur complement system, is solved using a block preconditioner with overlap between the blocks that is referred to as Algebraic Additive Schwarz. A fully algebraic coarse space is available for symmetric positive definite problems, that insures the numerical scalability of the preconditioner.
The parallel implementation is based on MPI+thread. Maphys relies on state-of-the art sparse and dense direct solvers.
MaPHyS is essentially a preconditioner that can be used to speed-up the convergence of any Krylov subspace method and is coupled with the ones implemented in the Fabulous package.
- Publications: Hierarchical hybrid sparse linear solver for multicore platforms – Robust coarse spaces for Abstract Schwarz preconditioners via generalized eigenproblems
- URL: https://gitlab.inria.fr/solverstack/maphys
PaStiX
Parallel Sparse matriX package
Keywords: Linear algebra – High-performance calculation – Factorisation – Sparse Matrices – Linear Systems Solver
Scientific Description: PaStiX is based on an efficient static scheduling and memory manager, in order to solve 3D problems with more than 50 million of unknowns. The mapping and scheduling algorithm handle a combination of 1D and 2D block distributions. A dynamic scheduling can also be applied to take care of NUMA architectures while taking into account very precisely the computational costs of the BLAS 3 primitives, the communication costs and the cost of local aggregations.
Functional Description: PaStiX is a scientific library that provides a high performance parallel solver for very large sparse linear systems based on block direct and block ILU(k) methods. It can handle low-rank compression techniques to reduce the computation and the memory complexity. Numerical algorithms are implemented in single or double precision (real or complex) for LLt, LDLt and LU factorization with static pivoting (for non symmetric matrices having a symmetric pattern). The PaStiX library uses the graph partitioning and sparse matrix block ordering packages Scotch or Metis.
The PaStiX solver is suitable for any heterogeneous parallel/distributed architecture when its performance is predictable, such as clusters of multicore nodes with GPU accelerators or KNL processors. In particular, we provide a high-performance version with a low memory overhead for multicore node architectures, which fully exploits the advantage of shared memory by using an hybrid MPI-thread implementation.
The solver also provides some low-rank compression methods to reduce the memory footprint and/or the time-to-solution.
- Partners: Université Bordeaux 1 – INP Bordeaux
- URL: https://gitlab.inria.fr/solverstack/pastix
PSBLAS-based preconditioners in LES simulation using Alya over the Bolund cliff
The mathematical model is the set of 3D incompressible unsteady Navier-Stokes equations for the Large Eddy Simulations (LES) of turbulent flows in a bounded domain with mixed boundary conditions. The LES formulation is closed by an appropriate expression for the subgrid-scale viscosity; in this analysis, the eddy-viscosity model proposed in (Vreman, 2004) is used.
Discretization is based on a low-dissipation mixed finite-element scheme, using linear finite elements both for velocity and pressure unknowns. A non-incremental fractional-step method is used to stabilize the pressure, whereas for the explicit time integration of the set of discrete equations a fourth order Runge-Kutta explicit method is applied (Lehmkuhl, 2019).
The pressure field is obtained at each step by solving a discretization of a Poisson-type equation.
The test case is based on the Bolund experiment, a classical benchmark for micro-scale atmospheric flow models over complex terrain; Bolund is a 12 m high, 130 m long and 75 m wide isolated hill in Denmark. It’s geological features result in a complex flow field that makes it apt for analyzing flow models (Bechmann, 2011). The Reynolds number based on the friction velocity is approximately.
To showcase the potentiality of the preconditioners implemented in MLD2P4 (D’Ambra 2010), the package of algebraic multigrid preconditioners based on PSBLAS (Filippone 2000), we run a weak scalability test fixing 2.9e4 dofs per core, for incresing number of cores up to 12288 cores and a mesh size up to 345276325 reaching approximately 0.35e9 dofs. At each time step, we solve the symmetric positive definite linear systems arising from the pressure equation employing the Conjugate Gradient (CG) method of PSBLAS, coupled with different preconditioners implemented in MLD2P4. We run simulations for a total of 20 time steps starting from the time equal to 1.5e-1.
We selected the diagonal preconditioner (AlyaDCG), for comparison aims with the diagonal preconditioner implemented in the original Alya code and generally used for simulations, and a version of Deflated CG (AlyaDFCG) available from the original Alya code. From the PSBLAS/MLD2P4 libraries we selected a symmetric V-cycle employing an algebraic multilevel hierarchy with 4 levels built by applying the decoupled smoothed aggregation coarsening implemented in MLD2P4, 4 iterations of forward/backward Gauss-Seidel smoother at the intermediate levels and two different parallel iterative coarsest solvers: 4 iterations of the Block-Jacobi method with ILU(1) on the diagonal blocks (MLBJAC) and the CG method preconditioned by ILU(1) with a stopping criterion based on the reduction of the relative residual of 4 orders of magnitude or a maximum number of iterations equal to 30 (MLRKR).
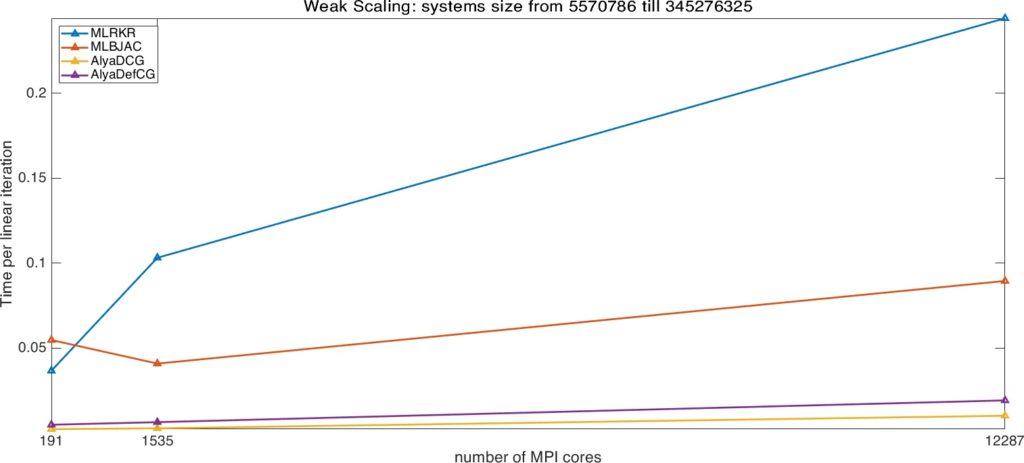
If we look at the time spent at each linear iteration, we see that the multilevel preconditioners show a very small increase. This shows a very good implementation scalability of the library code, which improves when the surface to volume effect is reduced, i.e. when the ratio between data communication and data computation is reduced. The time per iteration is not larger than 0.28 sec. on 12288 cores, corresponding to a worst-case time per dof of about 8.1e-10 sec. We also observe that MLBJAC has a smaller time per iteration than MLRKR, especially when the largest number of cores is used. This depends on the less data communication required by 4 iterations of the distributed Block-Jacobi method with respect to the preconditioned CG for the coarsest systems solution.
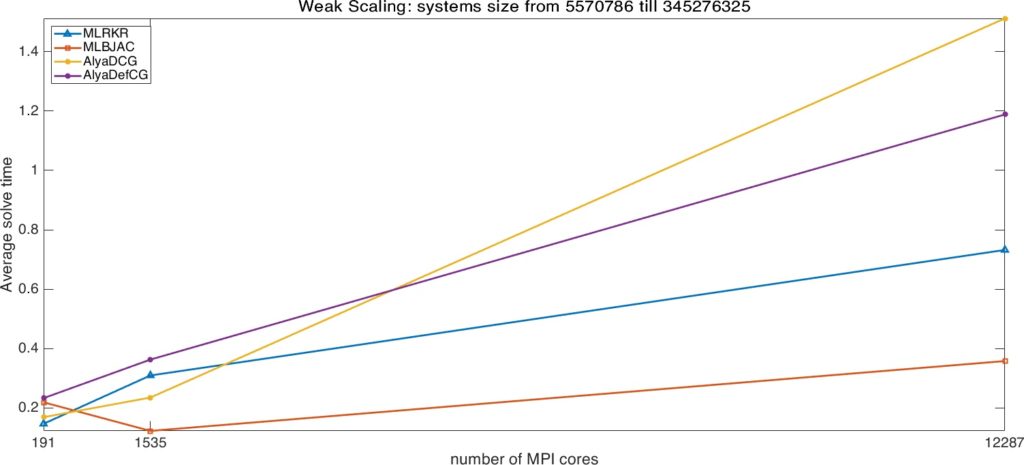
Indeed, the large reduction in the number of iterations produces smaller solution time both for MLBJAC and MLRKR with respect to the Alya original solvers. The cost of the preconditioner setup is largely amortized in using the same preconditioner for solving at each time step of the LES.
Bibliography
- P. D’Ambra, et al., “MLD2P4: a Package of Parallel Multilevel Algebraic Domain Decomposition Preconditioners in Fortran 95”, ACM Trans. on Math. Software, 37, 3 (2010), 30:1-30:23.
- S. Filippone, et al., “PSBLAS: A library for parallel linear algebra computation on sparse matrices”, ACM Trans. on Math. Software, 26, 4 (2000), 527-550.
- Vreman, A. W. “An eddy-viscosity subgrid-scale model for turbulent shear flow: Algebraic theory and applications.” Physics of fluids 16.10 (2004): 3670-3681.
- Lehmkuhl, Oriol, et al. “A low-dissipation finite element scheme for scale resolving simulations of turbulent flows.” Journal of Computational Physics 390 (2019): 51-65.
- Bechmann, Andreas, et al. “The Bolund experiment, part II: blind comparison of microscale flow models.” Boundary-layer meteorology 141.2 (2011): 245.
All the EoCoE-I and EoCoE-II publications are available here (openAIRE).
EoCoE II: Toward Exascale for Energy , Project ID: 824158
EoCoE, Grant/Award Number: 824158
